KTRニュース
株式会社KTRへのご依頼・お問合わせは、TEL:072-997-3471、
メール ktr@office.zaq.jp でも受け付けております。
過去配信済みのKTRニュース
 第001回「LD50(エルディーゴジュウ)」について
第001回「LD50(エルディーゴジュウ)」について 第005回「製品の安全性(有害物質について)」
第005回「製品の安全性(有害物質について)」 第013回「環境マネージメントシステム」について
第013回「環境マネージメントシステム」について 第015回「PBB(ピービービー),PBDE(ピービーディーイー)」について
第015回「PBB(ピービービー),PBDE(ピービーディーイー)」について 第025回「化学物質の安全性」について
第025回「化学物質の安全性」について 第030回「有機溶剤(ゆうきようざい)」について
第030回「有機溶剤(ゆうきようざい)」について 第031回「かび」とは何か
第031回「かび」とは何か 第036回「CAS 番号(キャス バンゴウ)」について
第036回「CAS 番号(キャス バンゴウ)」について 第038回「界面活性剤(かいめんかっせいざい)」について
第038回「界面活性剤(かいめんかっせいざい)」について 第040回「化学物質の安全性調査」について
第040回「化学物質の安全性調査」について 第043回「無毒性量(むどくせいりょう)」について
第043回「無毒性量(むどくせいりょう)」について 第046回「環境マーク」について
第046回「環境マーク」について 第051回「放射線の単位」について
第051回「放射線の単位」について 第053回「プラスチックの添加剤(てんかざい)」について
第053回「プラスチックの添加剤(てんかざい)」について 第054回「臭いとVOC(ブイオーシー)」について
第054回「臭いとVOC(ブイオーシー)」について 第068回「EN71-3の規制物質増える」
第068回「EN71-3の規制物質増える」 第074回「エコテック規格100」について
第074回「エコテック規格100」について 第081回「in vitro(イン・ビトロ)とin vivo(イン・ビボ)」について
第081回「in vitro(イン・ビトロ)とin vivo(イン・ビボ)」について 第083回「皮膚感作性(ひふかんさせい)」について
第083回「皮膚感作性(ひふかんさせい)」について 第084回「鉛毒(なまりどく)」について
第084回「鉛毒(なまりどく)」について 第104回「毒」について
第104回「毒」について 第106回「皮膚刺激性」について
第106回「皮膚刺激性」について 第108回「きのこ」について
第108回「きのこ」について 第112回「エコマーク」について
第112回「エコマーク」について 第117回「ワクチン」とは何か
第117回「ワクチン」とは何か 第014回「アクリル」について
第014回「アクリル」について 第024回「ボールタック試験(粘着性の試験)」について
第024回「ボールタック試験(粘着性の試験)」について 第037回「粘着剤」について 1
第037回「粘着剤」について 1 第044回「ゴム」について
第044回「ゴム」について 第056回「粘着テープ関係のJIS規格」について
第056回「粘着テープ関係のJIS規格」について 第058回「ボールタック、粘着力、保持力の関係」について
第058回「ボールタック、粘着力、保持力の関係」について 第063回「超撥水性(ちょうはっすいせい)」について
第063回「超撥水性(ちょうはっすいせい)」について 第075回「粘着剤」について 2
第075回「粘着剤」について 2 第090回「膠(にかわ)」について
第090回「膠(にかわ)」について 第101回「医療用粘着テープ」について
第101回「医療用粘着テープ」について 第109回「布テープの粘着力要素(試料幅、圧着力等の違い等)」について
第109回「布テープの粘着力要素(試料幅、圧着力等の違い等)」について 第111回「離型紙(りけいし)」について
第111回「離型紙(りけいし)」について 第113回「濡(ぬ)れ性(せい)」について
第113回「濡(ぬ)れ性(せい)」について 第006回「分析」について 1
第006回「分析」について 1 第021回「プラスチックの見分け方(赤外分析)」について1
第021回「プラスチックの見分け方(赤外分析)」について1 第027回「蛍光X線分析機」について
第027回「蛍光X線分析機」について 第028回「熱可塑性プラスチックの熱分析」について
第028回「熱可塑性プラスチックの熱分析」について 第041回「周期律表と蛍光X線分析」
第041回「周期律表と蛍光X線分析」 第052回「ガス-マス(GC-MS:ジーシー/マス)分析」について
第052回「ガス-マス(GC-MS:ジーシー/マス)分析」について 第059回「プラスチックの見分け方(赤外分析)」について2
第059回「プラスチックの見分け方(赤外分析)」について2 第060回「赤外分析」について
第060回「赤外分析」について 第067回「赤外線分析(IR)」について
第067回「赤外線分析(IR)」について 第092回「分析」について 2
第092回「分析」について 2 第093回「分析」について 3
第093回「分析」について 3 第119回「粘弾性(ねんだんせい);レオロジー」とは何か
第119回「粘弾性(ねんだんせい);レオロジー」とは何か 第120回「粘弾性(ねんだんせい);レオロジー」とは何か 2
第120回「粘弾性(ねんだんせい);レオロジー」とは何か 2 第002回「ストレスクラック」について
第002回「ストレスクラック」について 第016回「可塑剤(かそざい)」について
第016回「可塑剤(かそざい)」について 第017回「水と油はなぜ混ざらないのか」
第017回「水と油はなぜ混ざらないのか」 第023回「積層造形(ラピッドプロトタイピング)」について
第023回「積層造形(ラピッドプロトタイピング)」について 第032回「製品の耐久試験」について
第032回「製品の耐久試験」について  第035回「色」について
第035回「色」について 第050回「静電気」について
第050回「静電気」について 第055回「ウレタン」について
第055回「ウレタン」について 第057回「シリコン樹脂」について 1
第057回「シリコン樹脂」について 1 第066回「エラストマー」について
第066回「エラストマー」について  第077回「プラスチックの劣化(熱可塑性)」
第077回「プラスチックの劣化(熱可塑性)」 第078回「プラスチックの分子量を測定する」
第078回「プラスチックの分子量を測定する」 第082回「PET(ペット樹脂)」について
第082回「PET(ペット樹脂)」について 第085回「油」について
第085回「油」について 第096回「シリコン樹脂」について 2
第096回「シリコン樹脂」について 2 第107回「ポリビニールアルコール(ポバール)」について
第107回「ポリビニールアルコール(ポバール)」について 第110回「ポリマーアロイ」について
第110回「ポリマーアロイ」について 第115回「ウレタンジェル(耐震マット)」について
第115回「ウレタンジェル(耐震マット)」について 第121回「オレフィン樹脂」について
第121回「オレフィン樹脂」について 第004回「N(ニュートン)」について
第004回「N(ニュートン)」について 第007回「品質工学」(タグチメソッド)について 1
第007回「品質工学」(タグチメソッド)について 1  第008回「品質工学」(タグチメソッド)について 2
第008回「品質工学」(タグチメソッド)について 2  第009回「品質工学」(タグチメソッド)について 3
第009回「品質工学」(タグチメソッド)について 3  第026回「硬さ」について
第026回「硬さ」について 第034回「鉄の錆び」について
第034回「鉄の錆び」について 第039回「抜き取り検査」について
第039回「抜き取り検査」について 第042回「ロードセル(荷重測定器)」について
第042回「ロードセル(荷重測定器)」について 第045回「有限要素法(ゆうげんようそほう)<FEM>」について
第045回「有限要素法(ゆうげんようそほう)<FEM>」について 第061回「メッキ」について
第061回「メッキ」について 第062回「チタン」について
第062回「チタン」について 第065回「CEマーク」について
第065回「CEマーク」について 第069回「鉄(鋼)の焼き入れ」について
第069回「鉄(鋼)の焼き入れ」について 第072回「アルミニュウム」について
第072回「アルミニュウム」について 第076回「JIS(ジス)とは何か」
第076回「JIS(ジス)とは何か」 第089回「ISO(イソ、アイエスオー)」について
第089回「ISO(イソ、アイエスオー)」について 第091回「試験規格」について
第091回「試験規格」について 第094回「アレルギー」について 1
第094回「アレルギー」について 1 第095回「アレルギー」について 2
第095回「アレルギー」について 2 第097回「アレルギー(ゴム)」について 3
第097回「アレルギー(ゴム)」について 3 第098回「繊維製品の物性試験」について
第098回「繊維製品の物性試験」について 第099回「繊維製品の染色堅牢度試験」について
第099回「繊維製品の染色堅牢度試験」について 第100回「防水・耐水・撥水」について
第100回「防水・耐水・撥水」について 第102回「マイクロスコープ」について
第102回「マイクロスコープ」について 第105回「DHAとEPA」について
第105回「DHAとEPA」について 第114回「乳酸菌」について
第114回「乳酸菌」について 第116回「大理石(だいりせき)」について
第116回「大理石(だいりせき)」について 第118回「酵素(こうそ)」とは何か
第118回「酵素(こうそ)」とは何か 第010回「VOC(揮発性有機溶剤)シックハウス症候群」について
第010回「VOC(揮発性有機溶剤)シックハウス症候群」について 第011回「RoHS(ローズ)」について
第011回「RoHS(ローズ)」について 第018回「化審法(かしんほう)」について
第018回「化審法(かしんほう)」について 第020回「HACCP(ハサップ)」食品の安全性確保
第020回「HACCP(ハサップ)」食品の安全性確保 第022回「REACH(リーチ)」とは何か 1
第022回「REACH(リーチ)」とは何か 1 第029回「REACH(リーチ)」とは何か 2
第029回「REACH(リーチ)」とは何か 2 第047回「REACH(リーチ)」とは何か 3
第047回「REACH(リーチ)」とは何か 3 第073回「トスカ(TSCA)」について
第073回「トスカ(TSCA)」について 第086回「化学物質を規制する法律 1」
第086回「化学物質を規制する法律 1」 第087回「化学物質を規制する法律 2」
第087回「化学物質を規制する法律 2」 第088回「化学物質を規制する法律 3」
第088回「化学物質を規制する法律 3」KTRニュース動画
 株式会社KTRのYouTubeページ
株式会社KTRのYouTubeページ
youtube 最新回
youtube 最新回
youtube 動画配信リスト
第002回「ストレスクラック」について
第003回「促進試験」について
第004回「N(ニュートン)」について
第005回「製品の安全性(有害物質)」について
第010回「VOC(揮発性有機溶剤)シックハウス症候群」について
第011回「RoHS(ローズ」について
第012回「安全係数)」について
第013回「環境マネージメントシステム」について
第014回「アクリル」について
第016回「可塑剤」について
第017回「水と油はなぜ混ざらないのか」
第021回「プラスチックの見分け方(赤外分析)」について1
第023回「積層造形(ラピッドプロトタイピング)」について
第024回「ボールタック試験(粘着性の試験)」について
第025回「化学物質の安全性」について
第026回「硬さ」について
第027回「蛍光X線分析機」について
第028回「熱可塑性プラスチックの熱分析」について
第031回「かび」とは何か
第032回「製品の耐久試験」について
第033回「扇風機の寿命は何年か」
第035回「色」
第036回「CAS 番号(キャス バンゴウ)」について
第037回「粘着剤」について 1
第038回「界面活性剤(かいめんかっせいざい)」について
第041回「周期律表と蛍光X線分析」
第043回「無毒性量(むどくせいりょう)」について
第044回「ゴム」について
第046回「環境マーク」について
第048回「耐光試験(たいこうしけん)」について 1
第049回「耐光試験(たいこうしけん)」について 2
第052回「ガスーマス(GC-MS:ジーシー/マス)分析」について
第053回「プラスチックの添加剤」について
第054回「臭いとVOC(ブイオーシー)」について
第056回「粘着テープ関係のJIS規格」について
第058回「ボールタック、粘着力、保持力の関係」について
第059回「プラスチックの見分け方(赤外分析)」について2
第060回「赤外分析」について
第062回「チタン」について
第063回「超撥水性(ちょうはっすいせい)」について
第064回「ポリプロピレン(PP)の劣化」について
第066回「エラストマー」について
第067回「赤外線分析(IR)」について
第068回「EN71-3の規制物質増える」
第070回「ABS樹脂(プラスチック)の劣化」について
第073回「トスカ(TSCA)」について
第075回「粘着剤」について 2
第079回「内部応力(残留応力)」について
第081回「in vitro(イン・ビトロ)とin vivo(イン・ビボ)」について
第083回「皮膚感作性」について
第090回「膠(にかわ)」について
第098回「繊維製品の物性試験」について
第099回「繊維製品の染色堅牢度試験」について
第100回「防水・耐水・撥水」について
第101回「医療用粘着テープ」について
第102回「マイクロスコープ」について
第103回「粘着製品の老化試験」について
第104回「毒」について
第105回「DHAとEPA」について
第106回「皮膚刺激性」について
第107回「ポリビニールアルコール(ポバール)」について
第108回「きのこ」について
第109回「布テープの粘着力要素(試料幅、圧着力等の違い等)」について
第110回「ポリマーアロイ」について
第111回「離型紙(りけいし)」について
第112回「エコマーク」について
第113回「濡(ぬ)れ性(せい)」について
第114回「乳酸菌」について
第115回「ウレタンジェル(耐震マット)」について
第116回「大理石(だいりせき)」について
第117回「ワクチン」とは何か
第118回「酵素(こうそ)」とは何か
第119回「粘弾性(ねんだんせい);レオロジー」とは何か
第120回「粘弾性(ねんだんせい);レオロジー」とは何か 2
第121回「オレフィン樹脂」について
KTRニュース配信お申込み
第39回目
第39回「抜き取り検査」について
(1)<抜き取り検査とは>
抜き取り検査とはあるロットの中から、ある数のみを抜き出して、それの品質を見て
取りだした元のロットの品質を評価するものです。
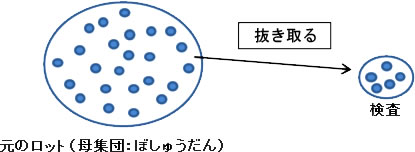
元のロットの製品の数を10000個とします。検査するサンプルの数は10個とします。
検査するサンプル(10個)で、元のロット(10000個)の品質を判断します。
元のロットから、検査する製品をランダムに抜き取ります。当然抜き取られたサンプルは良い製品もあれば、不良の製品も抜き取る場合もあります。
本当に、わずかな数のサンプル(10個)で、元のロット(10000個)の品質が判断できるのでしょうか。
これは、次に説明する考え方によって、ある確率で元のロットの品質を判断できることになります。
(2)<抜き取りの例題>
抜き取り検査の基礎をなす考えかたを説明いたします。
抜き取り検査は、n個のサンプルを抜き取ってサンプル1個ずつについて、良品、不良を判定して、不良品の数が決められた個数を超えた時、その元のロット全体を不合格とするものです。
ロット全体の不良率は不明であるが、仮に20%(本当はこんなに大きな不良率はありません)
とします。そうしますと、このロットから10個のサンプルを抜き取った場合、10個中、2個が不良になるはずである。
しかし、ロットの中から10個をランダムに抜き取った場合、良品を取りだす確率は8/10ですが、かならずしも8個良品であるとは限りません。
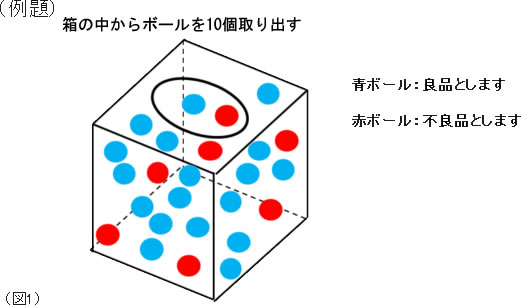
図1のような、縦、横、高さが30cmの箱を考えます。 次に、箱の中を見ないで、穴から手を入れてボールを1個取り出します。 |
          |
最初は青で、次も青、その次も青でした。4回目は赤でした。 箱の中から、10個のボールを順に取りだすことをもう一度行います。 |
          |
これは、先ほどより赤いボールの比率が大きくなりました。 このような、箱の中からボールを抜きだすことを、根気よく100回行います。 |
(3)<確率の説明>
少し専門的になりますが、確率の話をします。
上の例をさらに続けます。
箱の中には青いボールが8割、赤いボールが2割の割合で入っています。
今は箱の中から青いボールを取りだす確率を P(ピー:0.8)とします
次に、赤いボールを取りだす確率を Q(キュー:0.2)とします。
箱の中から、2個のボールを取りだす場合は、
|
|||||||||||||||||||||||||
| 上の4つの場合があります。それぞれが起こる確率は | |||||||||||||||||||||||||
| 青、青 | P × P = 0.8×0.8 =0.64 | ||||||||||||||||||||||||
| 青、赤 | P × Q = 0.8×0.2 =0.16 | ||||||||||||||||||||||||
| 赤、青 | Q × P = 0.2×0.8 =0.16 | ||||||||||||||||||||||||
| 赤、赤 | Q × Q = 0.2×0.2 =0.04 | ||||||||||||||||||||||||
| となります。それぞれが起こる確率は | |||||||||||||||||||||||||
| 青が2つの確率は | P2=0.8×0.8=0.64 | ||||||||||||||||||||||||
| 青が1つの確率は | 2PQ=2×0.8×0.2=0.32 | ||||||||||||||||||||||||
| 青が0の確率は | Q2=0.2×0.2=0.04 | ||||||||||||||||||||||||
| (合計 1.00) | |||||||||||||||||||||||||
| そして、上の組合せがすべての組合せをあらわしているので、 3つの確率の合計は、必ず1になります。 式にしますと、次のように表せます。 |
|||||||||||||||||||||||||
P2 + 2PQ + Q2 =1 |
|||||||||||||||||||||||||
| この式を書きなおすと | |||||||||||||||||||||||||
(P + Q)2=P2 + 2PQ + Q2=1 |
|||||||||||||||||||||||||
| になります。 | |||||||||||||||||||||||||
| 以上はボールを2個取り出す場合でしたが、 ボールを3個取り出す場合はつぎのようになります。 |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
| 青が3つの確率がP3、2つの確率が3P2Q,1つの確率が3PQ2、全部が赤の確率がQ3です。 | |||||||||||||||||||||||||
P3+3P2Q+3PQ2+Q3=1 |
|||||||||||||||||||||||||
| であると同時に | |||||||||||||||||||||||||
(P+Q)3=P3+3P2Q+3PQ2+Q3=1 |
|||||||||||||||||||||||||
| となります。 | |||||||||||||||||||||||||
(4)<取り出すボールを10個にした場合>
上のように、箱から取り出すボールの数を10個に増やすと、次のようになります。
赤ボールの数 |
代表的な組合せ |
組合せの数 |
割合 |
||||||||||
nCr |
|||||||||||||
| 0個 | 青、青、青、青、青、青、青、青、青、青 | 1通り | 0.00098 | ||||||||||
| 1個 |
|
10通り | 0.00977 | ||||||||||
| 2個 |
|
45通り | 0.04395 | ||||||||||
| 3個 |
|
120通り | 0.11719 | ||||||||||
| 4個 |
|
210通り | 0.20508 | ||||||||||
| 5個 |
|
252通り | 0.24609 | ||||||||||
| 6個 |
|
210通り | 0.20508 | ||||||||||
| 7個 |
|
120通り | 0.11719 | ||||||||||
| 8個 |
|
45通り | 0.04394 | ||||||||||
| 9個 |
|
10通り | 0.00977 | ||||||||||
| 10個 | 赤、赤、赤、赤、赤、赤、赤、赤、赤、赤 | 1通り | 0.00098 | ||||||||||
| 合計 | 1024通り | 1.00000 |
これを式で表しますと、つぎのようになります。
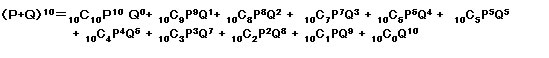
| この合計は必ず1になります。 この内、nCrはn個の中からr個取り出す組合せの数を表します。 これも式にしますと、次のようになります。 nCr = n!/r!×(n-r)! |
||
| C:コンビネーション(Combination(組合せ)のCである) !:階乗(かいじょう:nが大きくなるとn!が急に大きくなるので |
||
| 驚いてしまって、ビックリマークが使われている) n!=1×2×3×4×…×n |
||
今、青ボールの割合は0.8(P)、赤ボールの割合は0.2(Q)なので、上の式に代入してみます。
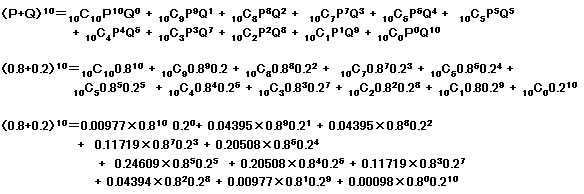
この計算は大変なので、計算していませんが、もし興味がある方は計算してください。
この合計は1になります。
たった10個抜き出すだけでも、膨大な計算になります。N数が80個になったらどのようになるのでしょうか。気が遠くなります。
(本当は簡易式があり、それで計算します。)
各々の値が、箱から10個取り出した場合の、赤いボールが1個の場合、2個の場合・・・・10個の場合の確率を表します。
赤いボールが2個の確率が一番多くなります。
(5)<抜き取り検査>
今までは、青いボールと赤いボールと言っていましたが、ここで品質管理の話に言いかえていきます。
最初の箱は検査ロットと言います。
青いボールは良品
赤いボールは不良品
10個を取りだすのは、サンプル数が10という意味です。
全数検査しない限り、全体の不良率は分かりません。
通常は全数検査をすることは費用と手間の関係で難しいので、抜き取り検査の結果で、元のロットの不良率を推定して、そのロットを合格にするのか、不合格にするのを決めます。
箱の中のボールを取りだす例からも、抜き取り検査ではロットの本当の不良率は分かりません。
しかも、通常は抜き取りを1回しかしません。検査する数も元のロットの数に比べて極めて少数です。
こんなことで、元のロットのことがわかるのでしょうか。
サイコロをふった場合、次にどの目がでるかはだれも分かりません。ただ、サイコロを1000回
ふった場合は、おそらく1から6までの目がほぼ均等に出るだろうと予測できます。
これと同じように、サンプルの結果は元のロットと同じような比率になるだろうとは予測できます。
ただ、確実に同じとは言えず、ある確率で同じような結果がでると考えることができます。
(6)<まとめ>
ある人は、抜き取り検査は20世紀最大の発明と言っています。大量生産で均一な品質のものが作れるのは、抜き取り検査が発明され、それが実施されたためだそうです。
あまり表面にはでてきませんが、我々が今の豊かな生活がいとなめるは、抜き取り検査が発明されためと考えることもできます。
YouTubeで一部のKTRニュースの動画配信中! 株式会社KTRのYouTubeページ






